Extended Kalman Filter
Implements a continuous-time extended Kalman filter, which is a Kalman filter for non-linear systems.
Library
Description
The Extended Kalman Filter block implements a continuous-time extended Kalman filter, which is a Kalman filter for non-linear state-space systems. The non-linear ordinary differential equation (ODE) for the state-space system must take the form:
| x_dot | = | f(x,u) |
| z | = | h(x) |
The variable, x, is the state vector. The variable, u, is the input vector, which is typically motor torques. The variable, z, is the measured signals which will be fed to the Kalman estimator. All quantities may be vectors.
The derivatives function, f(x,u), and the output function, h(x), must be implemented by the user using Simulink blocks. To enter the derivatives function, f(x,u), double-click on the block to open the block parameters dialog. Then click on the button to open the subsystem in which the derivatives function should be implemented. Be careful to get the dimensions of signals correct. If there are N states, then the output of the derivatives subsystem should be an N-element column vector (Simulink treats vectors as column vectors by default).
Likewise, to enter the output function, h(x), double-click on the block to open the block parameters dialog. Then click on the button to open the subsystem in which the output function should be implemented. Be careful to get the dimensions of signals correct. If there are M outputs, then the output of the output subsystem should be an M-element column vector (Simulink treats vectors as column vectors by default).
Likewise, to enter the derivatives Jacobian, F(x), double-click on the block to open the block parameters dialog. Then click on the button to open the subsystem in which the derivatives Jacobian function should be implemented. The derivatives Jacobian function is should produce a matrix of the partial derivatives of f(x,u) with respect to each state.
For example, if there are two states, x1 and x2, then:
| x1_dot | = | f1(x,u) |
| x2_dot | = | f2(x,u) |
and the Jacobian matrix will be an NxN matrix where N is the number of states:
| df1/dx1 | df1/dx2 |
| df2/dx1 | df2/dx2 |
Likewise, to enter the output Jacobian, H(x), double-click on the block to open the block parameters dialog. Then click on the button to open the subsystem in which the derivatives Jacobian function should be implemented. The derivatives Jacobian function is should produce a matrix of the partial derivatives of h(x) with respect to each state.
For example, if there are two outputs, z1 and z2, then:
| z1 | = | h1(x) |
| z2 | = | h2(x) |
and the Jacobian matrix will be an MxN matrix, where M is the number of outputs and N is the number of states:
| dh1/dx1 | dh1/dx2 |
| dh2/dx1 | dh2/dx2 |
| At no time should the input and output ports within the function subsystems be deleted. Doing so will break the block! |
Helpful Hints
Dimensions
The states, x, and outputs, z, are column vectors. When defining the various non-linear functions, be sure to output the
correct dimensions. Be especially careful that row vectors are output as a 1xW matrix and are not interpreted as 1D column vectors.
Input Ports
u
The input signal to the system.
z
The measurements from the system.
Output Ports
x_est
The estimated states of the system.
z_est
The filtered measurement from the system.
Data Type Support
This block accepts input of type double. The output is of type double.
Parameters and Dialog Box
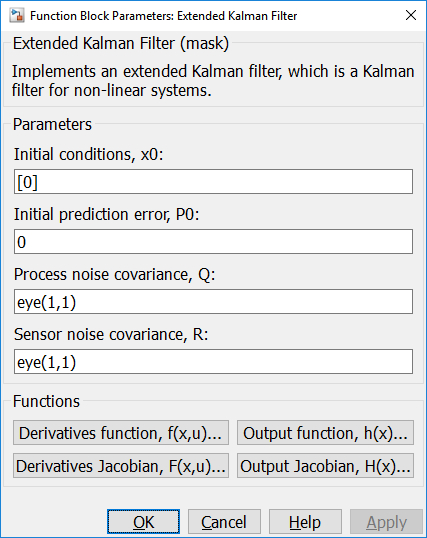
Initial conditions, x0
The initial states for the continuous-time system. This vector should have one element for each state, x. The dimension of this parameter must match the dimension of the x_dot output from the derivatives function, f(x,u). This parameter is treated as a column vector.
Initial prediction error, P0
The initial prediction error for the Kalman filter. It should be an NxN matrix, where N is the number of states. If a scalar is entered then it is treated as P0*ones(N,N).
Process noise covariance, Q
An NxN matrix, where N is the number of states. It should reflect the magnitude of the noise in the states. Diagonal terms correspond directly to the variance in the each state due to noise. Off-diagonal elements reflect noise coupling between states.
Sensor noise covariance, R
An MxM matrix, where M is the number of output elements in z. It should reflect the magnitude of the noise in the measurements. Diagonal terms correspond directly to the variance in each sensor reading due to noise. Off-diagonal elements reflect noise coupling between measured outputs.
Targets
|
Target Name |
Compatible* |
Model Referencing |
Comments |
|---|---|---|---|
|
Yes |
Yes |
||
|
Yes |
Yes |
||
|
Yes |
Yes |
||
|
Yes |
Yes |
||
|
Yes |
Yes |
||
|
Yes |
Yes |
||
|
Yes |
Yes |
||
|
Yes |
Yes |
||
|
Yes |
Yes |
||
|
Yes |
Yes |
||
|
Yes |
Yes |
||
|
Yes |
Yes |
||
|
Yes |
Yes |
||
|
Yes |
Yes |
Last fully supported in QUARC 2018. |
|
|
Rapid Simulation (RSIM) Target |
Yes |
Yes |
|
|
S-Function Target |
No |
N/A |
Old technology. Use model referencing instead. |
|
Normal simulation |
Yes |
Yes |
Copyright ©2024 Quanser Inc. This page was generated 2024-04-16. Submit feedback to Quanser about this page.
Link to this page.
