Inverse Modulus

Computes the accumulated output for signals which wrap. Optionally outputs the derivative of the input signal, accounting for wrapping.

Library

Description

The Inverse Modulus block computes the accumulated output for signals which wrap. For example, a potentiometer may output a voltage in the range 0V to 5V for each revolution of the potentiometer shaft. Hence, there's a point in the revolution of the potentiometer in which the voltage jumps from 5V to 0V or vice versa. Such discontinuities can be a problem for control algorithms. Furthermore, the number of revolutions turned is lost. This block provides a solution by detecting these discontinuities and adjusting the output to reflect the number of revolutions that have occurred. In the above example, the output of the Inverse Modulus block would not jump from 5V to 0V but would instead continue to increase beyond 5V. Likewise, when moving in the opposite direction, the output would not jump from 0V to 5V but would go negative.

A similar situation occurs when using the velocity of the signal which wraps. In the same example, if the potentiometer were used in a velocity or PD control application the velocity would jump whenever the output voltage wrapped between 0V and 5V. The Inverse Modulus block has an optional velocity output which eliminates this discontinuity in the time derivative of the input signal.

The only constraint upon this block is that it must be executed frequently enough that the input does not change by more than half the Modulus between executions. In other words, the sampling rate of the model must be more than twice the frequency of the input signal - the standard Nyquist criterion.

The Modulus refers to the modulus in modulo arithmetic, since an input signal which wraps is congruent to the unwrapped output. Mathmematically, the Inverse Modulus block computes the output such that the following relationship is satisfied:

in = (out - c) (mod Modulus) + c

where c is the minimum possible value of the input signal, in. The constant, c, allows for signed or unsigned input signals, or even arbitrary offsets. It is deduced by the block and does not need to be entered.

For example, consider an encoder with an 8-bit unsigned counter. Hence, the counter values may vary between 0 and 255. If the encoder rotates in the positive direction beyond a count of 255 then the count wraps immediately back to 0 and continues counting upward. Likewise, if the encoder rotates in the negative direction beyond a count of 0 then the count wraps immediately back to 255 and continues counting downward. If we had a signed counter of infinite range then it would never wrap. Let's call this the "unwrapped" count. Consider the values of the two counters when the shaft is rotating in the positive direction at 100 counts per sampling instant. The values are also shown in hexadecimal in parentheses because wrapping is equivalent to discarding all but the two least significant hexadecimal digits for an 8-bit counter.

The Inverse Modulus block calculates the unwrapped count in this table (the second column) given the values in the first column over time. Notice that the 8-bit values in the first column can be calculated from the unwrapped count in the second column using the modulo operation:

8-bit unsigned counter = unwrapped count (mod 256)

or in terms of the terminals of this block:

in = out (mod Modulus)

where the Modulus parameter is 256.

Note that the Inverse Modulus block handles signed input signals as well. Consider the same example, but this time let the encoder counter be a signed 8-bit counter. A signed 8-bit value ranges from -128 to +127. Hence, in this case, the sequence of count values will be:

As before, the Inverse Modulus block calculates the unwrapped count in this table (the second column) given the values in the first column over time. Notice that the 8-bit values in the first column can be calculated from the unwrapped count in the second column using the modulo operation:

8-bit signed counter = (unwrapped count + 128) (mod 256) - 128

or in terms of the terminals of this block:

in = (out - c) (mod Modulus) + c

where the Modulus parameter is 256 and the constant, c, is -128, the minimum possible value of the 8-bit signed encoder counter. Note that the Inverse Modulus block can calculate the unwrapped count without knowing the value of c.

Observe that for the 8-bit unsigned and 8-bit signed examples, the Modulus parameter is 256 in both cases.

The Inverse Modulus block is not limited to integer-valued input signals. For example, consider a multi-turn potentiometer whose voltage ranges from 0.0V to 5.0V and wraps with each revolution. Because the signal wraps regardless of the sensor technology used to measure the voltage, the Modulus parameter should be set to the voltage range of 5. The resolution of the A/D converter used to measure the voltage is irrelevant in this case.

The same formula:

in = (out - c) (mod Modulus) + c

applies but the modulo operation is real-valued in this case. The following table shows the 5V potentiometer example with the voltage changing by 1.3V every sampling instant:

When deciding on the appropriate Modulus argument, be sure to account for the source of the wrapping. In the multi-turn potentiometer example, the potentiometer voltage will wrap independent of the sensor used to measure the voltage. Hence, the modulus should be determined by the voltages at which the potentiometer wraps, not the resolution of the A/D used to measure it. However, a 24-bit encoder will wrap because of the limited bit width of the encoder counter in the data acquisition card, not because of the number of pulses per revolution of the physical encoder. Hence, the modulus should be determined by the bit width of the encoder counter and is generally 2 ⁿ where n is the number of bits in the encoder counter.

Note that the Modulus parameter is not restricted to integer values. For example, a multi-turn potentiometer might produce a voltage ranging from 0.0V to 1.25V, in which case a modulus of 1.25 is appropriate.

The following table gives general guidelines for choosing the appropriate Modulus argument to get the desired results.

Input Ports

in

The input is a scalar or vector signal that wraps. The range over which it wraps is described the the Modulus parameter. Refer to the description of this block for details.

Output Ports

out

The output is an "unwrapped" version of the input signal.

vel

The velocity of the input signal, accounting for wrapping. The velocity is calculated using the Euler difference method and is not filtered.

wrap

The number of times the input signal has wrapped relative to the starting position. The output is a signed value in which the sign indicates the direction in which the input signal wrapped.

Data Type Support

This block accepts inputs of any of the standard Simulink data types except Boolean because it is not possible to determine whether a boolean signal wraps, given that it can only take on values of 0 or 1. The outputs are of type double.

Parameters and Dialog Box

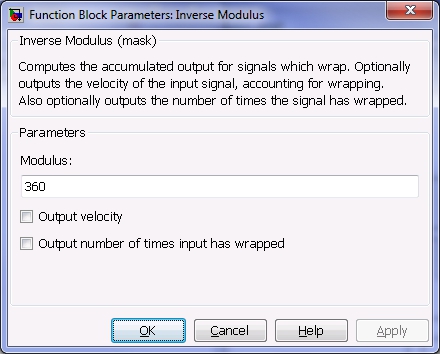
Modulus (tunable offline)

The modulus of congruence which describes the range of the input signal. See the description of this block for details.

Output velocity

Check this option to output the velocity of the input signal as an additional output.

Output number of times input has wrapped

Check this option to output the number of times the input signal has wrapped relative to the starting position as an additional output.

Targets

Copyright ©2024 Quanser Inc. This page was generated 2024-10-17. Submit feedback to Quanser about this page.

Link to this page.