Quaternion Rotate Jacobian
Computes the Jacobian of the quaternion rotation of q2 with respect to q1.
Library
MATLAB Command Line
Click to copy the following command line to the clipboard. Then paste it in the MATLAB Command Window:
qc_open_library('quarc_library/Math Operations/Quaternions')Description
The Quaternion Rotate Jacobian block computes the Jacobian of the quaternion rotation, q = q1⊗q2⊗q1-1, with respect to q1. If q1 is restricted to be a unit quaternion, then it computes the Jacobian of the quaternion rotation q = q1⊗q2⊗q1*. Select which Jacobian is to be computed via the Derivative with respect to parameter. These Jacobians can be useful for computing extended Kalman filters, for example.
Let q1 = (a1, b1, c1, d1) and q = (a, b, c, d). Then the Jacobian, J, of q with respect to q1 is:
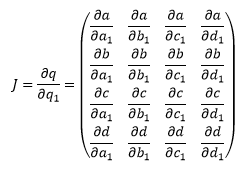
Input Ports
q1
The quaternion containing the angle and axis by which to rotate q2.
q2
The quaternion to rotate. This quaternion is typically a pure vector quaternion (zero scalar part) corresponding to a vector in 3D space.
Output Ports
J
The output is the Jacobian of the quaternion rotation q1⊗q2⊗q1-1 or q1⊗q2⊗q1*.
Data Type Support
This block accepts inputs of type double. The block output is
of type double.
Parameters and Dialog Box
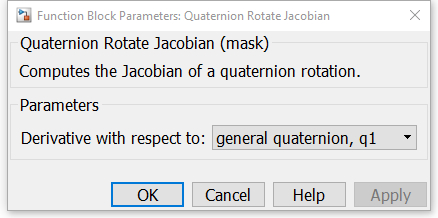
Derivative with respect to
If this option is set to general quaternion, q1 then this block does not assume that q1 is a unit quaternion, and computes the Jacobian of q = q1⊗q2⊗q1-1.
If this option is set to unit quaternion, q1 then this block assumes that q1 is a unit quaternion, and computes the Jacobian of q = q1⊗q2⊗q1* instead.
Note that the correct scenario must be chosen because the Jacobian is not the same in the two cases because q1-1≠q1* unless q1 is a unit quaternion.
Targets
|
Target Name |
Compatible* |
Model Referencing |
Comments |
|---|---|---|---|
|
Yes |
Yes |
||
|
Yes |
Yes |
||
|
Yes |
Yes |
||
|
Yes |
Yes |
||
|
Yes |
Yes |
||
|
Yes |
Yes |
||
|
Yes |
Yes |
||
|
Yes |
Yes |
||
|
Yes |
Yes |
||
|
Yes |
Yes |
||
|
Yes |
Yes |
||
|
Yes |
Yes |
||
|
Yes |
Yes |
||
|
Yes |
Yes |
Last fully supported in QUARC 2018. |
|
|
Rapid Simulation (RSIM) Target |
Yes |
Yes |
|
|
S-Function Target |
No |
N/A |
Old technology. Use model referencing instead. |
|
Normal simulation |
Yes |
Yes |
Copyright ©2024 Quanser Inc. This page was generated 2024-10-17. Submit feedback to Quanser about this page.
Link to this page.