Rotation Transformation :: QUARC Targets Library

navigation bar

Rotation Transformation

This block multiplies a homogeneous transformation matrix by a rotation matrix. The block can be configured to have either a fixed or variable rotation axis and a fixed or variable rotation angle.

Library

QUARC Targets/Math Operations/Homogeneous Transformations

Description

Rotation Transformation

This block multiplies an input homogeneous transformation matrix by a rotation matrix. The block can be configured to have either a fixed or variable rotation axis and a fixed or variable rotation angle by double clicking on the block and setting the appropriate parameters. The homogeneous rotation matrix is as follows:

  output = [(x^2*(1-cos(ang))+cos(ang))   (y*x*(1-cos(ang))-z*sin(ang)) (z*x*(1-cos(ang))+y*sin(ang)) 0
            (x*y*(1-cos(ang))+z*sin(ang)) (y^2*(1-cos(ang))+cos(ang))   (z*y*(1-cos(ang))-x*sin(ang)) 0
            (x*z*(1-cos(ang))-y*sin(ang)) (y*z*(1-cos(ang))+x*sin(ang)) (z^2*(1-cos(ang))+cos(ang))   0
             0                             0                             0                            1];

where x, y, and z are the elements of the rotation axis, and ang is the rotation angle. The input homogeneous transformation matrix is post-multiplied by this matrix.

Input Ports

4x4

This input takes the previous output from a homogeneous transformation block. If there are no prior transformation blocks then this input must be driven by a Identity Transformation block.

vec

If the block is configured to drive the rotation axis externally, then this port will be visible. The input should be a 3 element vector defining the axis of rotation. The vector will automatically be normalized by the block. The vector cannot be [0 0 0].

ang

If the block is configured to drive the rotation angle externally, then this port will be visible. The input should be a scalar to define the amount of rotation in radians about the defined rotation axis.

Output Ports

4x4

Outputs a 4x4 tranformation matrix.

Parameters and Dialog Box

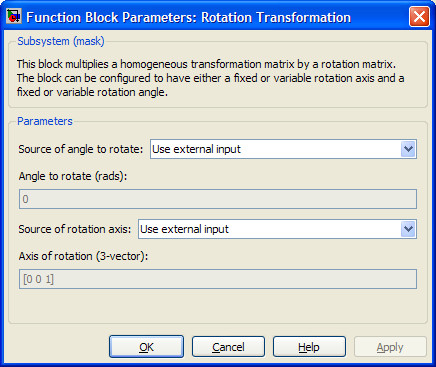
Rotation Transformation

Source of angle to rotate

Selects between internal and external sources for the rotation angle. If internal is selected, set the angle in the Angle to rotate field. If external is selected, you can connect a scalar input to the input port.

Angle to rotate

Sets the amount of rotation (in radians) to the fixed value entered in this field if the Source of angle to rotate is set to use the internal input.

Source of rotation axis

Selects between internal and external sources for the rotation axis. If internal is selected, set the axis in the Axis of rotation field. If external is selected, you can connect a 3 element vector to the input port.

Axis of rotation

Sets the axis of rotation to the fixed value entered in this field if the Source of rotation axis is set to use the internal input.

Targets

Target Name	Compatible*	Model Referencing	Comments
QUARC Win32 Target	Yes	Yes
QUARC Win64 Target	Yes	Yes
QUARC Linux Nvidia Target	Yes	Yes
QUARC Linux QBot Platform Target	Yes	Yes
QUARC Linux QCar 2 Target	Yes	Yes
QUARC Linux QDrone 2 Target	Yes	Yes
QUARC Linux Raspberry Pi 3 Target	Yes	Yes
QUARC Linux Raspberry Pi 4 Target	Yes	Yes
QUARC Linux RT ARMv7 Target	Yes	Yes
QUARC Linux x64 Target	Yes	Yes
QUARC Linux DuoVero Target	Yes	Yes
QUARC Linux DuoVero 2016 Target	Yes	Yes
QUARC Linux Verdex Target	Yes	Yes
QUARC QNX x86 Target	Yes	Yes	Last fully supported in QUARC 2018.
Rapid Simulation (RSIM) Target	Yes	Yes
S-Function Target	No	N/A	Old technology. Use model referencing instead.
Normal simulation	Yes	Yes

* Compatible means that the block can be compiled for the target.